재귀함수 분석 & 초 간단 트리 이론

Part 1 재귀함수

아래 코드를 보고 두 개의 코드 출력 결과를 생각해 보세요

코드 1

package baekjoon.tree;

public class RecursionPrac {

    public static void main(String[] args) {
        int n = 7;
        recursion1(n);
    }

    public static void recursion1(int n) {
        if(n == 0) return;

        System.out.println(n); // 출력하는 코드 입니다.
        recursion1(n - 1);
    }
}

코드 2

package baekjoon.tree;

public class RecursionPrac {

    public static void main(String[] args) {
        int n = 7
        recursion2(n);
    }

    public static void recursion2(int n) {
        if(n == 0) return;

        recursion2(n - 1);
        System.out.println(n); // 출력하는 코드 입니다.
    }
}

• 코드 1, 2 결과

코드 1 결과

코드 2 결과

<설명>

모든 언어(?)의 함수를 사용할 때 스택 자료구조를 활용합니다.

함수를 호출하면 Stack에 매개변수, 지역변수, 복귀주소를 넣고 함수를 실행합니다. 함수가 종료가 되면 Stack에 pop을 한 후 복귀주소가 적혀있는 곳으로 이동합니다.

코드 1번 같은 경우 출력을 하고 함수를 호출해서 스택에 넣기 때문에 7부터 출력을 다하게 됩니다.

코드 2번 같은 경우 함수를 호출해서 스택에 값을 넣고 출력을 하게 됩니다.

스택에는 그럼 7 → 6 → 5 → 4 → 3 → 2 → 1 이렇게 있고 스택은 LIFO의 특성을 가지고 있기 때문에 1부터 스택에 나와서 출력을 하게 됩니다.

 

Part 2 트리(전위순회, 중위순회, 후위순회)

트리란?

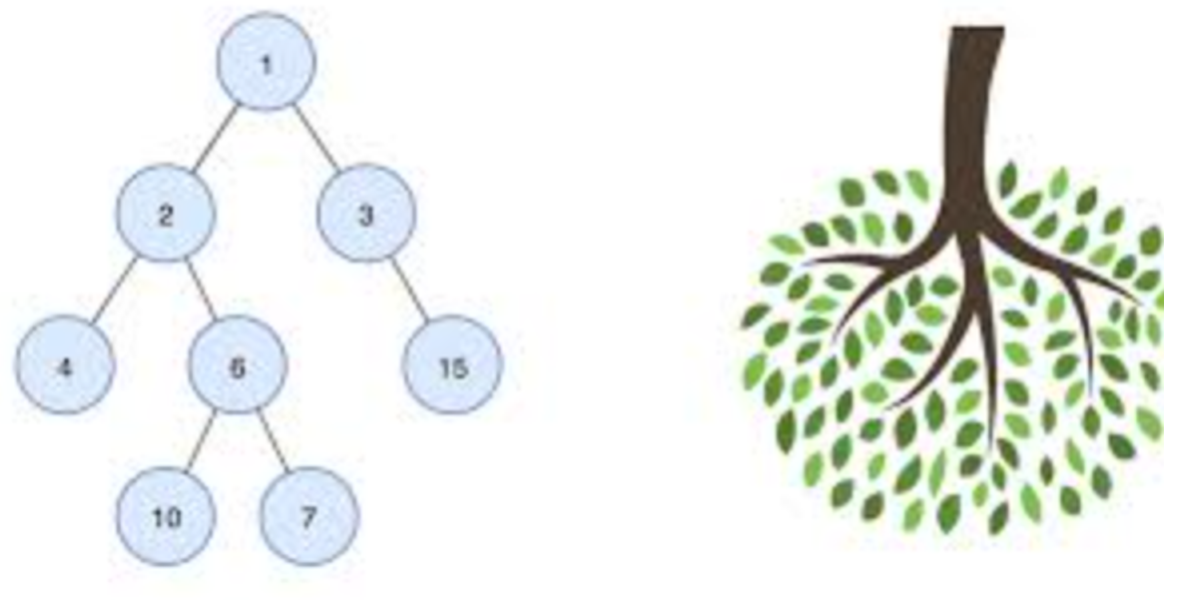
위 그림처럼 생긴 자료구조를 트리라고 합니다.

트리를 순회하는 방법에 따라 3가지 종류로 나뉩니다.

1. 전위순회(preorder) : 트리를 순회할 때 노드 - 왼쪽 자식 - 오른쪽 자식
2. 중위순회(inorder) : 왼쪽 자식 - 노드 - 오른쪽 자식
3. 후위순회(postorder) : 왼쪽 자식 - 오른쪽 자식 - 노드

예시

그래프 순회 코드

package baekjoon.tree;

public class TreeOrder {

    public static void main(String[] args) {

        int start = 1;
        System.out.println("print preorder");
        preorder(start);
        System.out.println();
        System.out.println("print inorder");
        inorder(start);
        System.out.println();
        System.out.println("print postorder");
        postorder(start);

    }

    public static void preorder(int v) {
        if(v > 7) return;
        System.out.print(v + " ");
        preorder(v * 2);
        preorder(v * 2 + 1);

    }
    public static void inorder(int v) {
        if(v > 7) return;
        inorder(v * 2);
        System.out.print(v + " ");
        inorder(v * 2 + 1);

    }public static void postorder(int v) {
        if(v > 7) return;
        postorder(v * 2);
        postorder(v * 2 + 1);
        System.out.print(v + " ");

    }

}

결과

 

<추가>

위 코드를 보고 그래프의 가지가 어떻게 뻗어나갔는지 아셨나요?

함수 내 재귀함수 호출하는 개수 = 가지의 개수입니다.

ex) 격자 미로 탐색